특징
- 완전이진트리의 일종이다.
- 여러 값들 중 최댓값 혹은 최솟값을 빠르게 찾아내기 위한 자료구조이다.
- 중복된 값을 허용한다.
- Max Heap은 가장 큰 값을 빠르게 찾기 위한 것이고, Min Heap은 가장 작은 값을 빠르게 찾기 위한 것이다.
※ 완전 이진 트리란?
여러 종류의 트리(Tree) 정리 (이진 트리, 전 이진 트리, 완전 이진 트리, 포화 이진 트리, 이진 탐
트리의 개념 - 노드로 이루어진 자료구조로 스택이나 큐 같은 선형 구조가 아닌 비선형 자료구조임. - 계층적 관계를 표현하는 자료구조임. 트리의 특성 - 하나의 루트 노드를 갖음. - 루트 노드
hyolls100.tistory.com
Map Heap
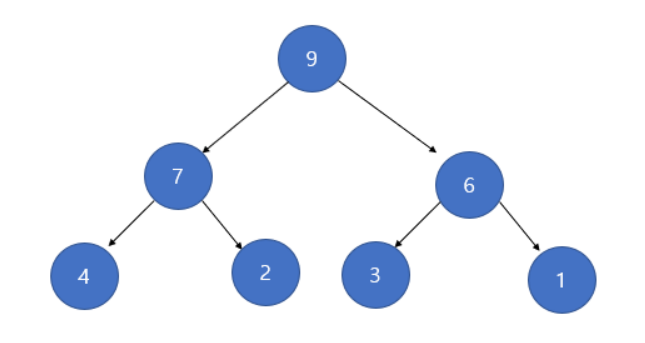
- Max Heap은 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리이다.
- 부모노드의 key >= 자식노드의 key (부등호 표시인 것은 중복허용이 되는 자료구조이므로)
Min Heap

- Min Heap은 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리이다.
- 부모노드의 key <= 자식노드의 key
Heap 구현

- Heap은 배열을 통해 쉽게 구현 가능하다 → 그 이유는 완전 이진 트리이기 때문이다. 완전 이진 트리 특성상 왼쪽부터 오른쪽으로 차곡차곡 노드가 저장되므로 배열의 구조를 사용할 수 있다.
- 0번 인덱스를 사용하지 않는다. → 그 이유는 다음과 같이 구현을 쉽게 하기 위함이다.(인덱스를 통해 노드를 접근)
▶ 부모 노드의 인덱스 = 자식 노드의 인덱스 / 2 (ex : 4번 노드의 부모노드 : 2번 노드)
▶ 왼쪽 자식 노드의 인덱스 = 부모 노드의 인덱스 * 2 (ex : 3번 노드의 왼쪽 자식 노드 : 6번 노드)
▶ 오른쪽 자식 노드의 인덱스 = 부모 노드의 인덱스 * 2 + 1 (ex : 3번 노드의 오른쪽 자식 노드 : 7번 노드)
Heap의 삽입
1. 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다. ( = 배열의 마지막에 원소를 추가한다. )
2. 새로운 노드를 부모 노드와 비교해서 교환해야 한다면 힙의 성질을 만족 할 때까지 교환한다.
★ 예를 들어 위의 Max Heap에 새로운 노드(key=8)을 추가한다고 하자.

첫 번째로 배열의 가장 마지막 위치에 새로운 원소 8을 추가한다.

두 번째로 부모노드인 4번 노드와 키 값을 비교하고 이 때 자식노드인 8번 노드가 키 값이 더 크므로(8>4) 부모노드와 위치를 교환한다.

마지막으로 부모노드인 2번 노드와 키 값을 비교하고 이 때 자식노드인 4번 노드가 키 값이 더 크므로(8>7) 부모노드와 위치를 교환한다. 그 다음으로는 부모노드인 1번 노드와 키 값을 비교했을 때 2번 노드가 키 값이 더 작으므로(8<9) 삽입과정이 종료된다.
※ Min Heap은 반대로 부모노드가 자식노드보다 작도록 교환하면 된다.
Heap의 삭제
Heap에서의 삭제는 루트 노드를 삭제하고 반환한다는 뜻이다.. 루트 노드의 의미는 Max Heap에서는 가장 큰 키 값을 가진 노드이고, Min Heap은 가장 작은 키 값을 가진 노드이다.
1. 루트노드를 삭제한다. (★나중에 값을 반환해야 하므로 따로 저장해놓음)
2. 삭제된 루트노드의 위치에 힙의 가장 마지막 노드를 가져온다.
3. 힙의 조건에 맞게 위치를 재설정한다. (이것을 heapify라고함)

루트 노드를 삭제하고 삭제된 루트 노드의 위치에 힙의 가장 마지막 노드를 가져온다.

힙의 조건에 맞게 위치를 재설정하는 과정으로 ★이때 주의할 점은 비교할 노드보다 큰 자식 노드가 2개 있을 때, 더 큰 값을 가진 자식 노드와 교환해야 한다는 것이다.
따라서 위에서는 index 1번 노드와 index 2번 노드가 교환한다. (8>6)

마찬가지로 위치를 재설정하는 과정을 거치면 삭제가 완료된다. Max Heap 의 조건을 만족하는 것을 확인 할 수 있다.
'CS 공부 > 자료구조' 카테고리의 다른 글
| 트리(Tree)의 순회 (전위/중위/후위 순회) (0) | 2023.08.10 |
|---|---|
| 여러 종류의 트리(Tree) 정리 (이진 트리, 전 이진 트리, 완전 이진 트리, 포화 이진 트리, 이진 탐색 트리) (0) | 2023.08.09 |
| 원형큐(Circular Queue)란? (0) | 2023.08.07 |
| Queue & Stack (0) | 2023.06.24 |
| Dynamic Array란? (0) | 2023.06.24 |