탄생 계기

이진탐색트리는 위 그림과 같이 한쪽으로 노드가 쏠릴 수가 있는 문제점이 있다. 10,9,8,7,6을 순서대로 삽입한다고 생각해보면 저런 형태의 트리가 만들어진다는 것을 알 수 있을 것이다. 이런 트리를 편향 트리라 하는데 이러한 형태에서 특정 값을 찾으려면 O(N)의 시간이 필요하다. 예를 들어 6을 찾으려면 모든 노드를 탐색해야지 찾을 수 있다. 따라서 성능이 매우 나빠지게 된다.
이진 탐색 트리 (BST-Binary Search Tree)
이진 탐색 트리란? 이진탐색트리(Binary Search Tree; BST)는 정렬된 tree이다. 어느 노드를 선택하든 해당 노드의 왼쪽 서브 트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로만 이루어져 있고, 오
hyolls100.tistory.com
이런 단점을 극복할 수 있는 자료구조가 균형을 맞춰주는 자가균형 이진탐색트리인데 이 중 하나가 Red-Black 트리이다. 균형이 잡히도록 해주는 트리로 최악의 경우에서도 모두 O(logn)이 보장되는 자료구조이다.
용어 정리

1) NIL 노드 (Null Leaf)
그림에서 사각형으로 된 리프 노드는 여기서 NIL 노드라고 부른다. 이 노드는 따로 key나 data를 포함하지 않으며 트리의 끝을 나타내는 노드로 실제 코드에서도 구현하지 않는 "완전 가상의 노드" 이다.
2) Internal 노드
internal 노드는 NIL이 아닌 나머지 노드라고 보면 된다.
리프 노드들을 성벽이라 생각하고, 그 위에 있는 노드들을 "성벽 내부 노드"라고 생각하면 된다.
3) Black Height
black height는 루트 노드에서부터 리프 노드까지 경로에 있는 검은 노드의 개수이다.
Red-Black 트리 성질
1. 각 노드는 레드 or 블랙이다.
2. 루트 노드와 모든 NIL 노드들은 항상 블랙이다.
3. 레드 노드는 자식으로 레드 노드가 있으면 안된. 레드 노드의 자식은 모두 블랙이다. == No Double Red (레드 노드가 연속으로 나올 수 없다.)
4. 블랙 노드의 자식은 레드이든 블랙이든 아무거나 상관없다.
5. 루트 노드에서 모든 리프 노드까지의 경로에 대해서 거치는 블랙 노드의 숫자는 같다. == Black Height가 같다.
Red-Black 트리 삽입과정
기본 이진트리 삽입에서 딱 2가지 스킬만 더 알고 있으면 된다. 우선 그에 앞서, 스킬을 사용해야 하는 경우가 있다.

현재 이런 이진트리가 있을 때, 값이 6인 노드를 삽입하면
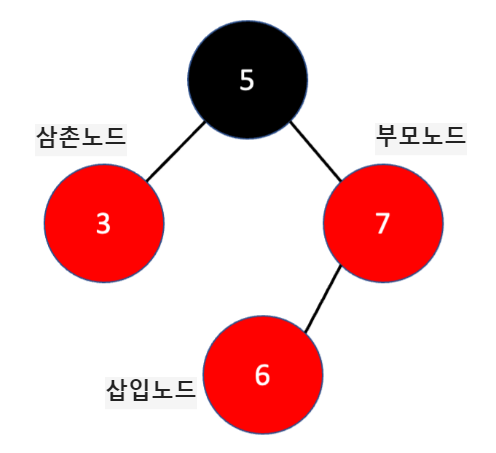
이진트리 성질에 의해 루트 노드보다 크므로 오른쪽 자식 노드로 이동 후, 왼쪽 자식으로 삽입된다.
하지만 앞서 말한 성질 3에 의해서 6, 7 노드는 연속된 빨간 노드, 즉 Double Red 상태가 되어서 일종의 기술이 필요하게 되는 것이다.
이때 사용하는 기술은 현재 삽입된 노드(여기서는 6)의 삼촌 노드(부모의 형제, 여기서는 3)의 색깔에 따라 나뉘는데
만약 삼촌 노드가 검정색이면 Restructing, 빨간색이면 Recoloring 기술을 사용해야 합니다. (예를 들어, 여기서는 삼촌 노드가 빨간색이므로 Recoloring을 사용해야한다.)
1.Restructing
★삼촌 노드가 검정색인 경우!!
1) 삽입된 노드와 그 부모, 그 조부모 노드를 오름차순으로 정렬한다.
2) 가운데 값을 부모로 만든 뒤, 나머지 둘을 자식으로 만들어준다.
3) 이때 부모는 블랙 노드, 두 자식들은 레드 노드로 만듭니다.
예를 들어,
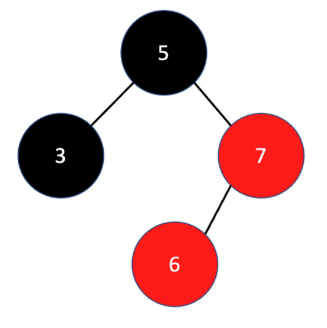
현재 노드 6이 삽입된 상태에서, Double Red가 된 경우에 삼촌 노드(3)가 블랙일 때 Restructing을 하게 된다.
이때 위에서 설명한 삽입노드, 부모노드, 조부모 노드는 오름차순 정렬되어 5,6,7이 되며 가운데 값은 6이다.
따라서 노드 6을 부모(블랙)로 둔 채, 두 자식(5, 7)을 자식(레드)으로 만들어준다.

하지만 원래 트리는 노드 3도 있었고, 3은 5의 왼쪽 자식이었다. 따라서 이를 그대로 다시 붙여준다.

Restructing 과정이 이로써 마무리된다. 결과적으로 Red-Black 트리의 모든 성질을 만족했음을 볼 수 있다.
새로운 노드가 삽입될 때, Restructing을 한다면 위치적으로 영향을 받는 노드는 딱 (자식-부모-조부모) 3가지이고, 만약 방금처럼 3 노드 밑에 자손이 있거나, 부모가 있는 경우 바꾼 후 다시 달아주면 된다.
따라서 다른 서브 트리에 영향을 미치지 않게 되는 것이다. 이것 자체의 시간 복잡도 역시 O(1)이고, 노드 삽입 과정에서 O(log N) 시간이 걸리기 때문에 총 시간 복잡도는 O(log N)이 된다.
2.Recoloring
★삼촌 노드가 빨간색인 경우!!
두 번째 기술은 앞서 설명한 Restructing와 다르게 노드의 색을 변경하는 방식이다.
1) 현재 삽입된 노드의 부모와 삼촌을 블랙으로 만든 후, 조부모를 레드로 만들어준다.
2) 만약 조부모가 루트 노드가 아니라면, 조부모의 부모가 레드일 수 있고, 이는 다시 Double Red 상황을 일으킬 수 있어 다시 한번 위로 돌아가 두 가지 기술에 대해 고민해봐야 한다. (propagation)
예를 들어,

시작은 노드 17이 삽입된 상황이다.
여기서 원래대로라면 Red-Black 트리의 균형성을 위해 위와 같은 트리가 나올 수 없지만, 설명을 위해 저 서브 트리 자체에만 집중을 해보자.
노드 17의 삼촌 노드는 노드 9이며 레드이다. Double Red이므로 Recoloring 조건을 만족합니다.
조부모를 레드, 부모와 삼촌을 블랙으로 바꿉니다.

이러면 나머지 노드는 조건을 만족하지만, 7-15 노드에서 Double Red 현상이 다시 한번 나타나게 된다.
따라서 이때는 노드 15가 삽입되었다는 가정하에 다시 한번 두 기술을 두고 고민해보는 것이다.
삼촌이 노드 5(레드)이므로 다시 한 번 Recoloring을 해준다면,

다음과 같은 트리가 된다.
★하지만 이때 루트 노드가 블랙이 아니다. 이럴 때는 바로 루트 노드만 블랙으로 변환해주면 Recoloring 과정이 종료된다.

Recoloring 또한 한 번 작업하는 것은 O(1)이고, 만약 Double Red 현상이 중복될 시 전파(propagation) 현상으로 인해 높이만큼 작업을 더 할 수 있다. 정말 최악의 경우이고, 이 때도 시간 복잡도는 O(log N)입니다.
+) 삼촌이 없는 경우에는 어떻게 할까?
삼촌이 없는 경우, 조부모가 NIL 노드를 왼쪽 혹은 오른쪽 자식으로 가지고 있는 경우이다.
이때 NIL 노드 또한 블랙 노드이므로 Restructing을 수행해주면 된다.
활용
1) map in C++ STL
C++의 map은 중복을 허용하지 않는 (key, value) 쌍으로 이루어진 트리이다.
map의 내부 구현은 검색, 삽입, 삭제가 O(log n)으로 동작하는 RB Tree로 구성되어 있다.
2) TreeMap in Java 8
Java 8 이전, 기존 LinkedList를 사용하던 충돌 방지 해시 로직 기반의 TreeMap을 RB Tree로 구현하였다. 그 결과 조회의 시간 복잡도가 O(N) → O(log N)이 되었다고 한다.
이외에도 Linux kernel에서의 Completely Fair Scheduler(CFS), epoll 등이 RB Tree를 사용한다고 한다.
※ Red-Black 트리 시뮬레이터
Red/Black Tree Visualization
www.cs.usfca.edu
'CS 공부 > 자료구조' 카테고리의 다른 글
| AVL 트리 & Red-Black 트리 비교 (0) | 2023.08.11 |
|---|---|
| AVL 트리 - 성질/삽입방법/활용 (0) | 2023.08.10 |
| 이진 탐색 트리 (BST-Binary Search Tree) (0) | 2023.08.10 |
| 트리(Tree)의 순회 (전위/중위/후위 순회) (0) | 2023.08.10 |
| 여러 종류의 트리(Tree) 정리 (이진 트리, 전 이진 트리, 완전 이진 트리, 포화 이진 트리, 이진 탐색 트리) (0) | 2023.08.09 |